Next: Some Analytically Soluble Problems Up: Brief Review of Quantum Previous: Linear Vector Spaces in

Postulates of Quantum Mechanics

In this section, we will present six postulates of quantum mechanics. Again, we follow the presentation of McQuarrie [1], with the exception of postulate 6, which McQuarrie does not include. A few of the postulates have already been discussed in section 3.

Postulate 1. The state of a quantum mechanical system is completely specified by a function $\Psi({\bf r}, t)$ that depends on the coordinates of the particle(s) and on time. This function, called the wave function or state function, has the important property that $\Psi^{*}({\bf r}, t) \Psi({\bf r}, t) d\tau$ is the probability that the particle lies in the volume element $d\tau$ located at ${\bf r}$ at time t.

The wavefunction must satisfy certain mathematical conditions because of this probabilistic interpretation. For the case of a single particle, the probability of finding it somewhere is 1, so that we have the normalization condition

$\begin{displaymath}\int_{-\infty}^{\infty} \Psi^{*}({\bf r}, t) \Psi({\bf r}, t) d\tau = 1 \end{displaymath}$

(110)

It is customary to also normalize many-particle wavefunctions to 1.² The wavefunction must also be single-valued, continuous, and finite.

Postulate 2. In any measurement of the observable associated with operator $\hat{A}$ , the only values that will ever be observed are the eigenvalues a, which satisfy the eigenvalue equation

$\begin{displaymath}\hat{A} \Psi = a \Psi \end{displaymath}$

(111)

This postulate captures the central point of quantum mechanics--the values of dynamical variables can be quantized (although it is still possible to have a continuum of eigenvalues in the case of unbound states). If the system is in an eigenstate of $\hat{A}$ with eigenvalue a, then any measurement of the quantity A will yield a.

Although measurements must always yield an eigenvalue, the state does not have to be an eigenstate of $\hat{A}$ . An arbitrary state can be expanded in the complete set of eigenvectors of $\hat{A}$ ( $\hat{A} \Psi_i = a_i \Psi_i)$ as

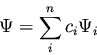$\begin{displaymath}\Psi = \sum_i^{n} c_i \Psi_i \end{displaymath}$

(112)

where n may go to infinity. In this case we only know that the measurement of A will yield one of the values a_i, but we don't know which one. However, we do know the probability that eigenvalue a_i will occur--it is the absolute value squared of the coefficient, |c_i|² (cf. section 3.1.4). This leads to our third postulate.

Postulate 3. If a system is in a state described by a normalized wave function $\Psi$ , then the average value of the observable corresponding to $\hat{A}$ is given by

$\begin{displaymath}<A> = \int_{-\infty}^{\infty} \Psi^{*} \hat{A} \Psi d\tau \end{displaymath}$

(113)

Postulate 4. To every observable in classical mechanics there corresponds a linear, Hermitian operator in quantum mechanics.

This postulate comes about because of the considerations raised in section 3.1.5: if we require that the expectation value of an operator $\hat{A}$ is real, then $\hat{A}$ must be a Hermitian operator. Some common operators occuring in quantum mechanics are collected in Table 1.

**Table 1:** Physical observables and their corresponding quantum operators (single particle)
Observable	Observable	Operator	Operator
Name	Symbol	Symbol	Operation
Position	${\bf r}$	$\hat{\bf r}$	Multiply by ${\bf r}$
Momentum	${\bf p}$	$\hat{\bf p}$	$-i \hbar \left( \hat{i} \frac{\partial}{\partial x} + \hat{j} \frac{\partial}{\partial y} + \hat{k} \frac{\partial}{\partial z} \right)$
Kinetic energy	T	$\hat{T}$	$- \frac{\hbar^2}{2m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right)$
Potential energy	$V({\bf r})$	$\hat{V}({\bf r})$	Multiply by $V({\bf r})$
Total energy	E	$\hat{H}$	$- \frac{\hbar^2}{2m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right) + V({\bf r})$
Angular momentum	l_x	$\hat{l}_x$	$-i \hbar \left( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y} \right)$
	l_y	$\hat{l}_y$	$-i \hbar \left( z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z} \right)$
	l_z	$\hat{l}_z$	$-i \hbar \left( x \frac{\partial}{\partial y} - y \frac{\partial}{\partial x} \right)$

Postulate 5. The wavefunction or state function of a system evolves in time according to the time-dependent Schrödinger equation

$\begin{displaymath}\hat{H} \Psi({\bf r}, t) = i \hbar \frac{\partial \Psi}{\partial t} \end{displaymath}$

(114)

The central equation of quantum mechanics must be accepted as a postulate, as discussed in section 2.2.

Postulate 6. The total wavefunction must be antisymmetric with respect to the interchange of all coordinates of one fermion with those of another. Electronic spin must be included in this set of coordinates.

The Pauli exclusion principle is a direct result of this antisymmetry principle. We will later see that Slater determinants provide a convenient means of enforcing this property on electronic wavefunctions.

Next: Some Analytically Soluble Problems Up: Brief Review of Quantum Previous: Linear Vector Spaces in