


Next: Mathematical Background
Up: The Schrödinger Equation
Previous: The Time-Independent Schrödinger Equation
The Time-Dependent Schrödinger Equation
We are now ready to consider the time-dependent Schrödinger
equation. Although we were able to derive the single-particle
time-independent Schrödinger equation starting from the classical
wave equation and the de Broglie relation, the time-dependent
Schrödinger equation cannot be derived using elementary methods and
is generally given as a postulate of quantum mechanics. It is
possible to show that the time-dependent equation is at least reasonable if not derivable, but the arguments are rather involved
(cf. Merzbacher [2], Section 3.2; Levine
[3], Section 1.4).
The single-particle three-dimensional time-dependent Schrödinger
equation is
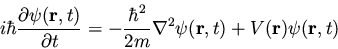 |
(21) |
where V is assumed to be a real function and represents the
potential energy of the system (a complex function V will act as a
source or sink for probability, as shown in Merzbacher
[2], problem 4.1). Wave Mechanics is the
branch of quantum mechanics with equation (21) as its
dynamical law. Note that equation (21) does not yet
account for spin or relativistic effects.
Of course the time-dependent equation can be used to derive the
time-independent equation. If we write the wavefunction as a product
of spatial and temporal terms,
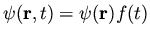 ,
then equation (21) becomes
,
then equation (21) becomes
![\begin{displaymath}\psi({\bf r}) i \hbar \frac{df(t)}{dt} = f(t) \left[
- \frac{\hbar^2}{2m} \nabla^2 + V({\bf r}) \right] \psi({\bf r})
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img36.png) |
(22) |
or
![\begin{displaymath}\frac{i \hbar}{f(t)} \frac{df}{dt} = \frac{1}{\psi({\bf r})} ...
...frac{\hbar^2}{2m} \nabla^2 + V({\bf r}) \right] \psi({\bf r})
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img37.png) |
(23) |
Since the left-hand side is a function of t only and the right hand
side is a function of 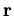 only, the two sides must equal a constant.
If we tentatively designate this constant E (since the right-hand side
clearly must have the dimensions of energy), then we extract two
ordinary differential equations, namely
only, the two sides must equal a constant.
If we tentatively designate this constant E (since the right-hand side
clearly must have the dimensions of energy), then we extract two
ordinary differential equations, namely
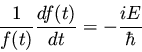 |
(24) |
and
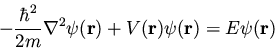 |
(25) |
The latter equation is once again the time-independent Schrödinger equation.
The former equation is easily solved to yield
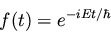 |
(26) |
The Hamiltonian in equation (25) is a Hermitian operator,
and the eigenvalues of a Hermitian operator must be real, so E is
real. This means that the solutions f(t) are purely oscillatory,
since f(t) never changes in magnitude (recall Euler's formula
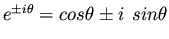 ). Thus
if
). Thus
if
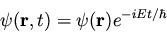 |
(27) |
then the total wave function
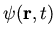 differs from
differs from
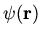 only by a phase factor of constant magnitude.
There are some interesting consequences of this. First of all, the
quantity
only by a phase factor of constant magnitude.
There are some interesting consequences of this. First of all, the
quantity
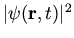 is time independent, as we can easily
show:
is time independent, as we can easily
show:
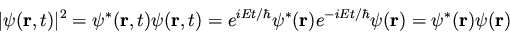 |
(28) |
Secondly, the expectation value for any time-independent operator is
also time-independent, if
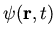 satisfies equation
(27). By the same reasoning applied above,
satisfies equation
(27). By the same reasoning applied above,
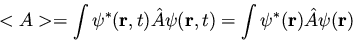 |
(29) |
For these reasons, wave functions of the form (27) are
called stationary states. The state
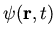 is
``stationary,'' but the particle it describes is not!
is
``stationary,'' but the particle it describes is not!
Of course equation (27) represents a particular solution
to equation (21). The general solution to equation
(21) will be a linear combination of these particular
solutions, i.e.
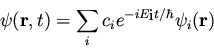 |
(30) |



Next: Mathematical Background
Up: The Schrödinger Equation
Previous: The Time-Independent Schrödinger Equation
![]() ,
then equation (21) becomes
,
then equation (21) becomes
![\begin{displaymath}\psi({\bf r}) i \hbar \frac{df(t)}{dt} = f(t) \left[
- \frac{\hbar^2}{2m} \nabla^2 + V({\bf r}) \right] \psi({\bf r})
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img36.png)
![\begin{displaymath}\frac{i \hbar}{f(t)} \frac{df}{dt} = \frac{1}{\psi({\bf r})} ...
...frac{\hbar^2}{2m} \nabla^2 + V({\bf r}) \right] \psi({\bf r})
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img37.png)
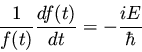
![]() ). Thus
if
). Thus
if