The Time-Independent Schrödinger Equation

Next: The Time-Dependent Schrödinger Equation Up: The Schrödinger Equation Previous: The Schrödinger Equation

The Time-Independent Schrödinger Equation

Here we follow the treatment of McQuarrie [1], Section 3-1. We start with the one-dimensional classical wave equation,

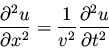$\begin{displaymath} \frac{\partial^2u}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2u}{\partial t^2} \end{displaymath}$

(10)

By introducing the separation of variables

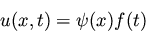$\begin{displaymath}u(x,t) = \psi(x)f(t) \end{displaymath}$

(11)

we obtain

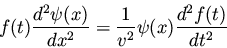$\begin{displaymath}f(t) \frac{d^2 \psi(x)}{dx^2} = \frac{1}{v^2} \psi(x) \frac{d^2f(t)}{dt^2} \end{displaymath}$

(12)

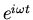If we introduce one of the standard wave equation solutions for f(t)such as $e^{i\omega t}$ (the constant can be taken care of later in the normalization), we obtain

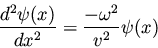$\begin{displaymath} \frac{d^2\psi(x)}{dx^2} = \frac{-\omega^2}{v^2} \psi(x) \end{displaymath}$

(13)

Now we have an ordinary differential equation describing the spatial amplitude of the matter wave as a function of position. The energy of a particle is the sum of kinetic and potential parts

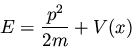$\begin{displaymath}E = \frac{p^2}{2m} + V(x) \end{displaymath}$

(14)

which can be solved for the momentum, p, to obtain

$\begin{displaymath}p = \{ 2m [ E - V(x) ] \} ^{1/2} \end{displaymath}$

(15)

Now we can use the de Broglie formula (4) to get an expression for the wavelength

$\begin{displaymath}\lambda = \frac{h}{p} = \frac{h}{\{ 2m [ E - V(x) ] \}^{1/2}} \end{displaymath}$

(16)

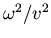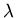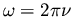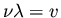The term $\omega^2/v^2$ in equation (13) can be rewritten in terms of $\lambda$ if we recall that $\omega = 2 \pi \nu$ and $\nu \lambda = v$ .

$\begin{displaymath}\frac{\omega^2}{v^2} = \frac{4 \pi^2 \nu^2}{v^2} = \frac{4\pi^2}{\lambda^2} = \frac{2m[E - V(x)]}{\hbar^2} \end{displaymath}$

(17)

When this result is substituted into equation (13) we obtain the famous time-independent Schrödinger equation

$\begin{displaymath}\frac{d^2\psi(x)}{dx^2} + \frac{2m}{\hbar^2} [ E - V(x)]\psi(x) = 0 \end{displaymath}$

(18)

which is almost always written in the form

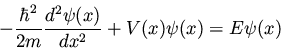$\begin{displaymath}-\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2} + V(x)\psi(x) = E\psi(x) \end{displaymath}$

(19)

This single-particle one-dimensional equation can easily be extended to the case of three dimensions, where it becomes

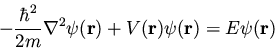$\begin{displaymath}-\frac{\hbar^2}{2m} \nabla^2\psi({\bf r}) + V({\bf r}) \psi({\bf r}) = E \psi({\bf r}) \end{displaymath}$

(20)

A two-body problem can also be treated by this equation if the mass m is replaced with a reduced mass 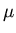$\mu$ .

It is important to point out that this analogy with the classical wave equation only goes so far. We cannot, for instance, derive the time-dependent Schrödinger equation in an analogous fashion (for instance, that equation involves the partial first derivative with respect to time instead of the partial second derivative). In fact, Schrödinger presented his time-independent equation first, and then went back and postulated the more general time-dependent equation.

Next: The Time-Dependent Schrödinger Equation Up: The Schrödinger Equation Previous: The Schrödinger Equation