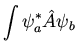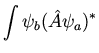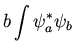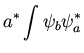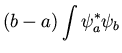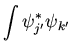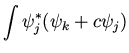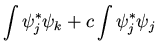


Next: Unitary Operators
Up: Operators
Previous: Eigenfunctions and Eigenvalues
Hermitian Operators
As mentioned previously, the expectation value of an operator 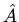 is
given by
is
given by
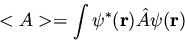 |
(55) |
and all physical observables are represented by such
expectation values. Obviously, the value of a physical observable such
as energy or density must be real, so we require <A> to be real.
This means that we must have
<A> = <A>*, or
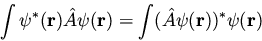 |
(56) |
Operators 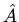 which satisfy this condition are called Hermitian.
One can also show that for a Hermitian operator,
which satisfy this condition are called Hermitian.
One can also show that for a Hermitian operator,
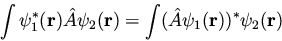 |
(57) |
for any two states 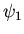 and
and 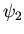 .
.
An important property of Hermitian operators is that their eigenvalues
are real. We can see this as follows: if we have an eigenfunction of
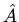 with eigenvalue a, i.e.
with eigenvalue a, i.e.
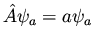 ,
then
for a Hermitian operator
,
then
for a Hermitian operator 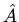
Since
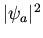 is never negative, we must have either a = a* or
is never negative, we must have either a = a* or
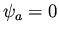 .
Since
.
Since
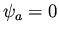 is not an acceptable wavefunction,
a = a*, so a is real.
is not an acceptable wavefunction,
a = a*, so a is real.
Another important property of Hermitian operators is that their
eigenvectors are orthogonal (or can be chosen to be so). Suppose that
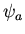 and
and 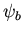 are eigenfunctions of
are eigenfunctions of 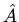 with eigenvalues
a and b, with
with eigenvalues
a and b, with 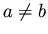 .
If
.
If 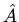 is Hermitian then
is Hermitian then
since a = a* as shown above. Because we assumed 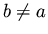 ,
we must
have
,
we must
have
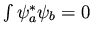 ,
i.e.
,
i.e. 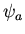 and
and 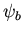 are
orthogonal. Thus we have shown that eigenfunctions of a Hermitian operator
with different eigenvalues are orthogonal. In the case of degeneracy
(more than one eigenfunction with the same eigenvalue), we can choose
the eigenfunctions to be orthogonal. We can easily show this for the
case of two eigenfunctions of
are
orthogonal. Thus we have shown that eigenfunctions of a Hermitian operator
with different eigenvalues are orthogonal. In the case of degeneracy
(more than one eigenfunction with the same eigenvalue), we can choose
the eigenfunctions to be orthogonal. We can easily show this for the
case of two eigenfunctions of 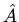 with the same eigenvalue. Suppose
we have
with the same eigenvalue. Suppose
we have
We now want to take linear combinations of 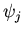 and
and 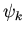 to form two
new eigenfunctions
to form two
new eigenfunctions 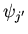 and
and 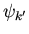 ,
where
,
where
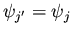 and
and
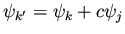 .
Now we want
.
Now we want 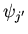 and
and 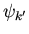 to be orthogonal, so
to be orthogonal, so
Thus we merely need to choose
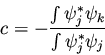 |
(62) |
and we obtain orthogonal eigenfunctions. This Schmidt-orthogonalization
procedure can be extended to the case of n-fold degeneracy, so we have shown
that for a Hermitian operator, the eigenvectors can be made orthogonal.



Next: Unitary Operators
Up: Operators
Previous: Eigenfunctions and Eigenvalues
![]() with eigenvalue a, i.e.
with eigenvalue a, i.e.
![]() ,
then
for a Hermitian operator
,
then
for a Hermitian operator ![]()
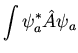
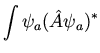
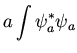
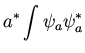
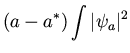
![]() and
and ![]() are eigenfunctions of
are eigenfunctions of ![]() with eigenvalues
a and b, with
with eigenvalues
a and b, with ![]() .
If
.
If ![]() is Hermitian then
is Hermitian then