Next: Operators and Quantum Mechanics
Up: Mathematical Background
Previous: Mathematical Background
Levine [3] defines an operator as ``a rule that
transforms a given function into another function'' (p. 33). The
differentation operator d/dx is an example--it transforms a
differentiable function f(x) into another function f'(x). Other
examples include integration, the square root, and so forth. Numbers
can also be considered as operators (they multiply a function).
McQuarrie [1] gives an even more general definition
for an operator: ``An operator is a symbol that tells you to do
something with whatever follows the symbol'' (p. 79). Perhaps this
definition is more appropriate if we want to refer to the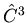 
operator acting on NH3, for example.