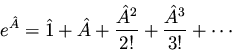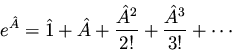


Next: Linear Operators
Up: Operators
Previous: Operators and Quantum Mechanics
Basic Properties of Operators
Most of the properties of operators are obvious, but they are summarized
below for completeness.
- The sum and difference of two operators
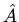 and
and
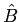 are given by
are given by
- The product of two operators is defined by
![\begin{displaymath}\hat{A} \hat{B} f \equiv \hat{A} [ \hat{B} f ]
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img58.png) |
(35) |
- Two operators are equal if
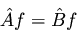 |
(36) |
for all functions f.
- The identity operator
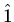 does nothing (or multiplies by 1)
does nothing (or multiplies by 1)
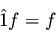 |
(37) |
A common mathematical trick is to write this operator as a sum over a
complete set of states (more on this later).
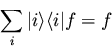 |
(38) |
- The associative law holds for operators
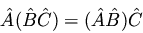 |
(39) |
- The commutative law does not generally hold for operators.
In general,
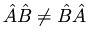 .
It is convenient to
define the quantity
.
It is convenient to
define the quantity
![\begin{displaymath}[\hat{A}, \hat{B}]\equiv \hat{A} \hat{B} - \hat{B} \hat{A}
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img65.png) |
(40) |
which is called the commutator of 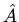 and
and 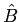 .
Note
that the order matters, so that
.
Note
that the order matters, so that
![$[ \hat{A}, \hat{B}] = - [ \hat{B}, \hat{A}]$](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img66.png) .
If
.
If 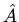 and
and 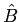 happen to commute, then
happen to commute, then
![$[\hat{A}, \hat{B}] = 0$](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img67.png) .
.
- The n-th power of an operator
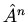 is defined as nsuccessive applications of the operator, e.g.
is defined as nsuccessive applications of the operator, e.g.
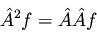 |
(41) |
- The exponential of an operator
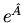 is defined via
the power series
is defined via
the power series
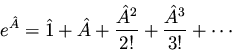 |
(42) |



Next: Linear Operators
Up: Operators
Previous: Operators and Quantum Mechanics