


Next: Postulates of Quantum Mechanics
Up: Mathematical Background
Previous: Commutators in Quantum Mechanics
We have observed that most operators in quantum mechanics are linear
operators. This is fortunate because it allows us to represent
quantum mechanical operators as matrices and wavefunctions as vectors
in some linear vector space. Since computers are particularly good at
performing operations common in linear algebra (multiplication of a
matrix times a vector, etc.), this is quite advantageous from a
practical standpoint.
In an n-dimensional space we may expand any vector 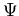 as a linear
combination of basis vectors
as a linear
combination of basis vectors
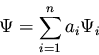 |
(80) |
For a general vector space, the coefficients ai may be complex; thus
one should not be too quick to draw parallels to the expansion
of vectors in three-dimensional Euclidean space. The coefficients ai
are referred to as the ``components'' of the state vector 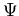 ,
and
for a given basis, the components of a vector specify it completely.
The components of the sum of two vectors are the sums of the components.
If
,
and
for a given basis, the components of a vector specify it completely.
The components of the sum of two vectors are the sums of the components.
If
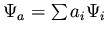 and
and
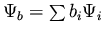 then
then
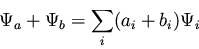 |
(81) |
and similarly
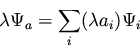 |
(82) |
The scalar product of two vectors is a complex number denoted by
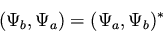 |
(83) |
where we have used the standard linear-algebra notation. If we also
require that
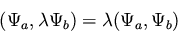 |
(84) |
then it follows that
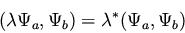 |
(85) |
We also require that
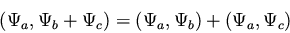 |
(86) |
If the scalar product vanishes (and if neither vector in the product is
the null vector) then the two vectors are orthogonal.
Generally the basis is chosen to be orthonormal, such that
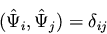 |
(87) |
In this case, we can write the scalar product of two arbitrary vectors
as
This can also be written in vector notation as
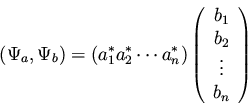 |
(89) |
It is useful at this point to introduce Dirac's bra-ket notation.
We define a ``bra'' as
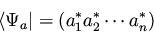 |
(90) |
and a ``ket'' as
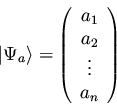 |
(91) |
A bra to the left of a ket implies a scalar product, so
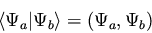 |
(92) |
Sometimes in superficial treatments of Dirac notation, the symbol
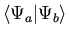 is defined alternatively as
is defined alternatively as
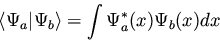 |
(93) |
This is equivalent to the above definition if we make the connections
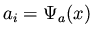 and
and
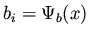 .
This means that our basis
vectors are every possible value of x. Since x is continuous,
the sum is replaced by an integral (see Szabo and Ostlund
[4] , exercise 1.17). Often only the subscript of
the vector is used to denote a bra or ket; we may have written the
above equation as
.
This means that our basis
vectors are every possible value of x. Since x is continuous,
the sum is replaced by an integral (see Szabo and Ostlund
[4] , exercise 1.17). Often only the subscript of
the vector is used to denote a bra or ket; we may have written the
above equation as
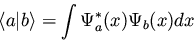 |
(94) |
Now we turn our attention to matrix representations of operators. An
operator 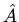 can be characterized by its effect on the basis
vectors. The action of
can be characterized by its effect on the basis
vectors. The action of 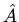 on a basis vector
on a basis vector
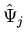 yields some new vector
yields some new vector 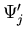 which can be expanded in terms of the
basis vectors so long as we have a complete basis set.
which can be expanded in terms of the
basis vectors so long as we have a complete basis set.
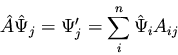 |
(95) |
If we know the effect of 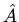 on the basis vectors, then we know the
effect of
on the basis vectors, then we know the
effect of 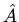 on any arbitrary vector because of the linearity
of
on any arbitrary vector because of the linearity
of 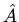 .
.
or
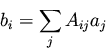 |
(97) |
This may be written in matrix notation as
 |
(98) |
We can obtain the coefficients Aij by taking the inner product of
both sides of equation 95 with
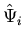 ,
yielding
,
yielding
since
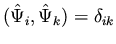 due to the orthonormality
of the basis. In bra-ket notation, we may write
due to the orthonormality
of the basis. In bra-ket notation, we may write
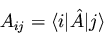 |
(100) |
where i and j denote two basis vectors. This use of bra-ket
notation is consistent with its earlier use if we realize that
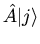 is just another vector
is just another vector
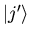 .
.
It is easy to show that for a linear operator 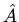 ,
the inner
product
,
the inner
product
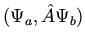 for two general vectors (not
necessarily basis vectors)
for two general vectors (not
necessarily basis vectors) 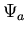 and
and 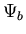 is given by
is given by
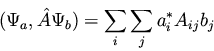 |
(101) |
or in matrix notation
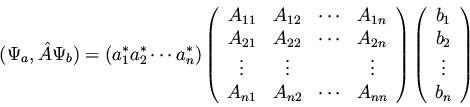 |
(102) |
By analogy to equation (93), we may generally write
this inner product in the form
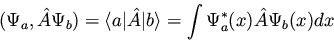 |
(103) |
Previously, we noted that
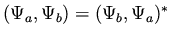 ,
or
,
or
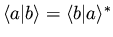 .
Thus we can see also that
.
Thus we can see also that
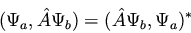 |
(104) |
We now define the adjoint of an operator 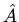 ,
denoted by
,
denoted by
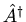 ,
as that linear operator for which
,
as that linear operator for which
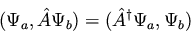 |
(105) |
That is, we can make an operator act backwards into ``bra'' space
if we take it's adjoint.
With this definition, we can further see that
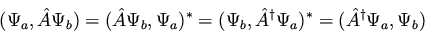 |
(106) |
or, in bra-ket notation,
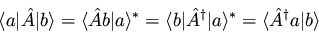 |
(107) |
If we pick
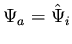 and
and
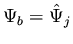 (i.e.,
if we pick two basis vectors), then we obtain
(i.e.,
if we pick two basis vectors), then we obtain
But this is precisely the condition for the elements of a matrix and its
adjoint! Thus the adjoint of the matrix representation of 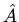 is
the same as the matrix representation of
is
the same as the matrix representation of
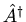 .
.
This correspondence between operators and their matrix representations
goes quite far, although of course the specific matrix representation
depends on the choice of basis. For instance, we know from linear
algebra that if a matrix and its adjoint are the same, then the matrix
is called Hermitian. The same is true of the operators; if
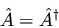 |
(109) |
then 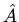 is a Hermitian operator, and all of the special properties
of Hermitian operators apply to
is a Hermitian operator, and all of the special properties
of Hermitian operators apply to  or its matrix representation.
or its matrix representation.



Next: Postulates of Quantum Mechanics
Up: Mathematical Background
Previous: Commutators in Quantum Mechanics
![]() as a linear
combination of basis vectors
as a linear
combination of basis vectors
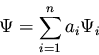
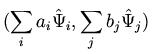
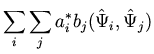
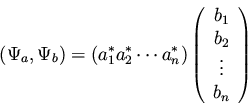
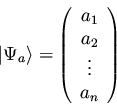
![]() is defined alternatively as
is defined alternatively as
![]() can be characterized by its effect on the basis
vectors. The action of
can be characterized by its effect on the basis
vectors. The action of ![]() on a basis vector
on a basis vector
![]() yields some new vector
yields some new vector ![]() which can be expanded in terms of the
basis vectors so long as we have a complete basis set.
which can be expanded in terms of the
basis vectors so long as we have a complete basis set.
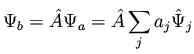
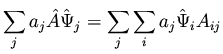
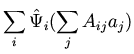
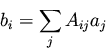

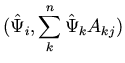
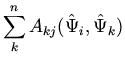
![]() ,
the inner
product
,
the inner
product
![]() for two general vectors (not
necessarily basis vectors)
for two general vectors (not
necessarily basis vectors) ![]() and
and ![]() is given by
is given by
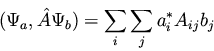
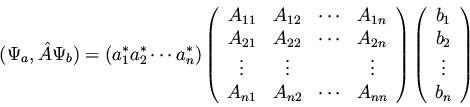
![]() ,
or
,
or
![]() .
Thus we can see also that
.
Thus we can see also that