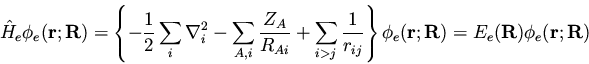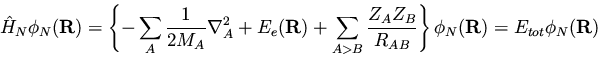


Next: Separation of the Nuclear
Up: Molecular Quantum Mechanics
Previous: The Molecular Hamiltonian
We know that if a Hamiltonian is separable into two or more terms,
then the total eigenfunctions are products of the individual
eigenfunctions of the separated Hamiltonian terms, and the total
eigenvalues are sums of individual eigenvalues of the separated
Hamiltonian terms.
Consider, for example, a Hamiltonian which is separable into two
terms, one involving coordinate q1 and the other involving coordinate
q2.
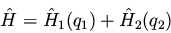 |
(135) |
with the overall Schrödinger equation being
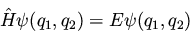 |
(136) |
If we assume that the total wavefunction can be written in the form
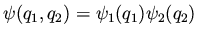 ,
where
,
where
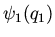 and
and
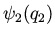 are eigenfunctions of
are eigenfunctions of 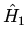 and
and 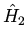 with
eigenvalues E1 and E2, then
with
eigenvalues E1 and E2, then
Thus the eigenfunctions of 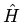 are products of the eigenfunctions
of
are products of the eigenfunctions
of 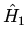 and
and 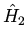 ,
and the eigenvalues are the sums of
eigenvalues of
,
and the eigenvalues are the sums of
eigenvalues of 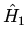 and
and 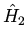 .
.
If we examine the nonrelativistic Hamiltonian (134), we
see that the term
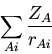 |
(138) |
prevents us from
cleanly separating the electronic and nuclear coordinates and writing
the total wavefunction as
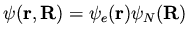 ,
where
,
where 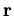 represents the set of all electronic coordinates, and
represents the set of all electronic coordinates, and
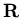 represents the set of all nuclear coordinates. The
Born-Oppenheimer approximation is to assume that this separation is
nevertheless approximately correct.
represents the set of all nuclear coordinates. The
Born-Oppenheimer approximation is to assume that this separation is
nevertheless approximately correct.
Qualitatively, the Born-Oppenheimer approximation rests on the fact
that the nuclei are much more massive than the electrons. This allows
us to say that the nuclei are nearly fixed with respect to electron
motion. We can fix 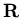 ,
the nuclear configuration, at some
value
,
the nuclear configuration, at some
value 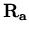 ,
and solve for
,
and solve for
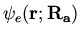 ;
the
electronic wavefunction depends only parametrically on
;
the
electronic wavefunction depends only parametrically on 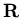 .
If
we do this for a range of
.
If
we do this for a range of 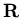 ,
we obtain the potential energy
curve along which the nuclei move.
,
we obtain the potential energy
curve along which the nuclei move.
We now show the mathematical details. Let us abbreviate the molecular
Hamiltonian as
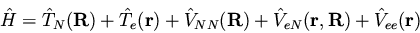 |
(139) |
where the meaning of the individual terms should be obvious.
Initially,
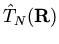 can be neglected since
can be neglected since 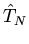 is
smaller than
is
smaller than 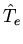 by a factor of MA / me, where me is
the mass of an electron. Thus for a fixed nuclear
configuration, we have
by a factor of MA / me, where me is
the mass of an electron. Thus for a fixed nuclear
configuration, we have
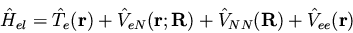 |
(140) |
such that
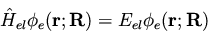 |
(141) |
This is the ``clamped-nuclei'' Schrödinger equation. Quite
frequently
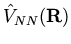 is neglected in the above equation,
which is justified since in this case
is neglected in the above equation,
which is justified since in this case 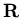 is just a parameter so
that
is just a parameter so
that
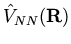 is just a constant and shifts the
eigenvalues only by some constant amount. Leaving
is just a constant and shifts the
eigenvalues only by some constant amount. Leaving
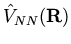 out of the electronic Schrödinger equation leads to a similar
equation,
out of the electronic Schrödinger equation leads to a similar
equation,
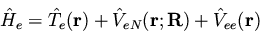 |
(142) |
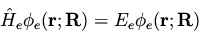 |
(143) |
where we have used a new subscript ``e'' on the electronic Hamiltonian and
energy to distinguish from the case where
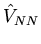 is included.
is included.
We now consider again the original Hamiltonian (139).
If we insert a wavefunction of the form
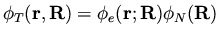 ,
we obtain
,
we obtain
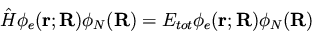 |
(144) |
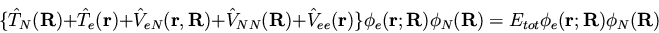 |
(145) |
Since 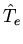 contains no
contains no 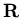 dependence,
dependence,
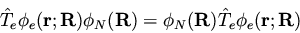 |
(146) |
However, we may not immediately assume
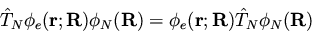 |
(147) |
(this point is tacitly assumed by most introductory textbooks).
By the chain rule,
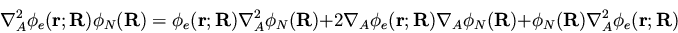 |
(148) |
Using these facts, along with the electronic Schrödinger equation,
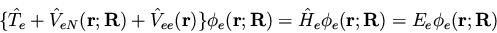 |
(149) |
we simplify (145) to
We must now estimate the magnitude of the last term in brackets.
Following Steinfeld [5], a typical contribution has
the form
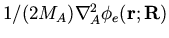 ,
but
,
but
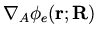 is of the
same order as
is of the
same order as
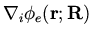 since the derivatives operate over
approximately the same dimensions. The latter is
since the derivatives operate over
approximately the same dimensions. The latter is
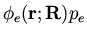 ,
with pe the momentum of an electron. Therefore
,
with pe the momentum of an electron. Therefore
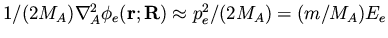 .
Since
.
Since
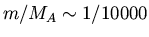 ,
the term in brackets can be dropped, giving
,
the term in brackets can be dropped, giving
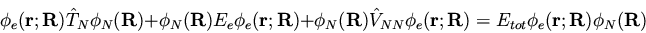 |
(151) |
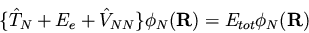 |
(152) |
This is the nuclear Shrodinger equation we anticipated--the nuclei
move in a potential set up by the electrons.
To summarize, the large difference in the relative masses of the
electrons and nuclei allows us to approximately separate the
wavefunction as a product of nuclear and electronic terms. The
electronic wavefucntion
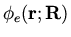 is solved for a given set of nuclear
coordinates,
is solved for a given set of nuclear
coordinates,
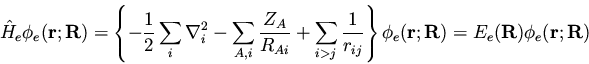 |
(153) |
and the electronic
energy obtained contributes a potential term to the motion of the nuclei
described by the nuclear wavefunction
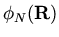 .
.
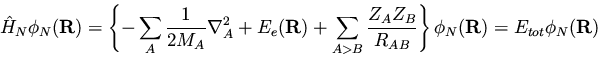 |
(154) |
As a final note, many textbooks, including Szabo and Ostlund
[4], mean total energy at fixed geometry when
they use the term ``total energy'' (i.e., they neglect the nuclear
kinetic energy). This is just Eel of equation (141),
which is also Ee plus the nuclear-nuclear repulsion. A somewhat
more detailed treatment of the Born-Oppenheimer approximation is given
elsewhere [6].



Next: Separation of the Nuclear
Up: Molecular Quantum Mechanics
Previous: The Molecular Hamiltonian
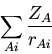
![]() ,
the nuclear configuration, at some
value
,
the nuclear configuration, at some
value ![]() ,
and solve for
,
and solve for
![]() ;
the
electronic wavefunction depends only parametrically on
;
the
electronic wavefunction depends only parametrically on ![]() .
If
we do this for a range of
.
If
we do this for a range of ![]() ,
we obtain the potential energy
curve along which the nuclei move.
,
we obtain the potential energy
curve along which the nuclei move.
![]() ,
we obtain
,
we obtain
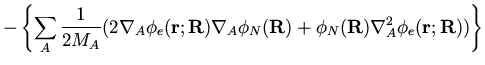
![]() ,
but
,
but
![]() is of the
same order as
is of the
same order as
![]() since the derivatives operate over
approximately the same dimensions. The latter is
since the derivatives operate over
approximately the same dimensions. The latter is
![]() ,
with pe the momentum of an electron. Therefore
,
with pe the momentum of an electron. Therefore
![]() .
Since
.
Since
![]() ,
the term in brackets can be dropped, giving
,
the term in brackets can be dropped, giving
![]() is solved for a given set of nuclear
coordinates,
is solved for a given set of nuclear
coordinates,