The Molecular Hamiltonian

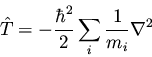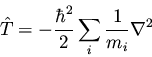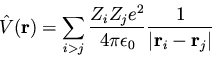
Next: The Born-Oppenheimer Approximation Up: Molecular Quantum Mechanics Previous: Molecular Quantum Mechanics

The Molecular Hamiltonian

We have noted before that the kinetic energy for a system of particles is

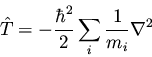$\begin{displaymath}\hat{T} = - \frac{\hbar^2}{2} \sum_i \frac{1}{m_i} \nabla^2 \end{displaymath}$

(132)

The potential energy for a system of charged particles is

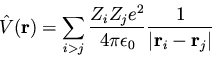$\begin{displaymath}\hat{V}({\bf r}) = \sum_{i>j} \frac{Z_i Z_j e^2}{4 \pi \epsilon_0} \frac{1}{\vert{\bf r}_i - {\bf r}_j\vert} \end{displaymath}$

(133)

For a molecule, it is reasonable to split the kinetic energy into two summations--one over electrons, and one over nuclei. Similarly, we can split the potential energy into terms representing interactions between nuclei, between electrons, or between electrons and nuclei. Using i and j to index electrons, and A and B to index nuclei, we have (in atomic units)

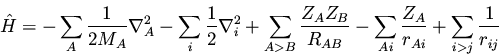$\begin{displaymath} \hat{H} = - \sum_A \frac{1}{2 M_A} \nabla^2_A - \sum_i \frac... ... - \sum_{Ai} \frac{Z_A}{r_{Ai}} + \sum_{i>j} \frac{1}{r_{ij}} \end{displaymath}$

(134)

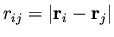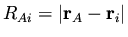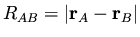where $r_{ij} = \vert{\bf r}_i - {\bf r}_j \vert$ , $R_{Ai} = \vert{\bf r}_A - {\bf r}_i\vert$ , and $R_{AB} = \vert{\bf r}_A - {\bf r}_B \vert$ . This is known as the ``exact'' nonrelativistic Hamiltonian in field-free space. However, it is important to remember that this Hamiltonian neglects at least two effects. Firstly, although the speed of an electron in a hydrogen atom is less than 1% of the speed of light, relativistic mass corrections can become appreciable for the inner electrons of heavier atoms. Secondly, we have neglected the spin-orbit effects. 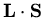From the point of view of an electron, it is being orbited by a nucleus which produces a magnetic field (proportional to L); this field interacts with the electron's magnetic moment (proportional to S), giving rise to a spin-orbit interaction (proportional to ${\bf L} \cdot {\bf S}$ for a diatomic.) Although spin-orbit effects can be important, they are generally neglected in quantum chemical calculations.

Next: The Born-Oppenheimer Approximation Up: Molecular Quantum Mechanics Previous: Molecular Quantum Mechanics