If we want to solve
![]() as
a matrix problem, we need to find a suitable linear vector space. Now
as
a matrix problem, we need to find a suitable linear vector space. Now
![]() is an N-electron function that must be
antisymmetric with respect to interchange of electronic coordinates.
As we just saw in the previous section, any such N-electron function
can be expressed exactly as a linear combination of Slater
determinants, within the space spanned by the set of orbitals
is an N-electron function that must be
antisymmetric with respect to interchange of electronic coordinates.
As we just saw in the previous section, any such N-electron function
can be expressed exactly as a linear combination of Slater
determinants, within the space spanned by the set of orbitals
![]() .
If we denote our Slater determinant basis
functions as
.
If we denote our Slater determinant basis
functions as
![]() ,
then we can express the eigenvectors as
,
then we can express the eigenvectors as
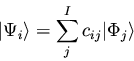 |
(167) |
If we solve this matrix equation,
![]() ,
in the space of all possible Slater determinants as
just described, then the procedure is called full
configuration-interaction, or full CI. A full CI constitues the exact solution to the time-independent Schrödinger equation within
the given space of the spin orbitals
,
in the space of all possible Slater determinants as
just described, then the procedure is called full
configuration-interaction, or full CI. A full CI constitues the exact solution to the time-independent Schrödinger equation within
the given space of the spin orbitals ![]() .
If we restrict the
N-electron basis set in some way, then we will solve Schrödinger's
equation approximately. The method is then called
``configuration interaction,'' where we have dropped the prefix
``full.'' For more information on configuration interaction, see the
lecture notes by the present author [7] or the review
article by Shavitt [8].
.
If we restrict the
N-electron basis set in some way, then we will solve Schrödinger's
equation approximately. The method is then called
``configuration interaction,'' where we have dropped the prefix
``full.'' For more information on configuration interaction, see the
lecture notes by the present author [7] or the review
article by Shavitt [8].