


Next: Matrix Mechanics
Up: Solving the Electronic Eigenvalue
Previous: Solving the Electronic Eigenvalue
Let us consider the nature of the electronic wavefunctions
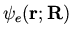 .
Since the electronic wavefunction depends only
parametrically on
.
Since the electronic wavefunction depends only
parametrically on 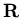 ,
we will suppress
,
we will suppress 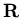 in our notation
from now on. What do we require of
in our notation
from now on. What do we require of
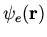 ? Recall that
? Recall that
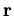 represents the set of all electronic coordinates, i.e.,
represents the set of all electronic coordinates, i.e.,
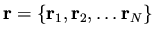 .
So far we have
left out one important item--we need to include the spin of each
electron. We can define a new variable
.
So far we have
left out one important item--we need to include the spin of each
electron. We can define a new variable 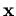 which represents the
set of all four coordinates associated with an electron: three spatial
coordinates
which represents the
set of all four coordinates associated with an electron: three spatial
coordinates 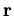 ,
and one spin coordinate
,
and one spin coordinate 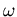 ,
i.e.,
,
i.e.,
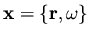 .
.
Thus we write the electronic wavefunction as
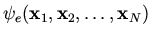 .
Why have we been able to avoid including
spin until now? Because the non-relativistic Hamiltonian does not
include spin. Nevertheless, spin must be included so that the
electronic wavefunction can satisfy a very important requirement,
which is the antisymmetry principle (see Postulate 6 in Section
4). This principle states that for a system of fermions, the
wavefunction must be antisymmetric with respect to the interchange of
all (space and spin) coordinates of one fermion with those of
another. That is,
.
Why have we been able to avoid including
spin until now? Because the non-relativistic Hamiltonian does not
include spin. Nevertheless, spin must be included so that the
electronic wavefunction can satisfy a very important requirement,
which is the antisymmetry principle (see Postulate 6 in Section
4). This principle states that for a system of fermions, the
wavefunction must be antisymmetric with respect to the interchange of
all (space and spin) coordinates of one fermion with those of
another. That is,
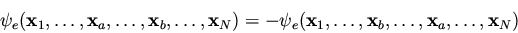 |
(156) |
The Pauli exclusion principle is a direct consequence of the antisymmetry
principle.
A very important step in simplifying
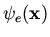 is to expand it
in terms of a set of one-electron functions, or ``orbitals.'' This
makes the electronic Schrödinger equation considerably easier to
deal with.3 A spin orbital is a function of
the space and spin coordinates of a single electron, while a spatial orbital is a function of a single electron's spatial
coordinates only. We can write a spin orbital as a product of a
spatial orbital one of the two spin functions
is to expand it
in terms of a set of one-electron functions, or ``orbitals.'' This
makes the electronic Schrödinger equation considerably easier to
deal with.3 A spin orbital is a function of
the space and spin coordinates of a single electron, while a spatial orbital is a function of a single electron's spatial
coordinates only. We can write a spin orbital as a product of a
spatial orbital one of the two spin functions
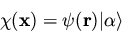 |
(157) |
or
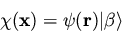 |
(158) |
Note that for a given spatial orbital
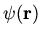 ,
we can form
two spin orbitals, one with
,
we can form
two spin orbitals, one with 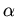 spin, and one with
spin, and one with 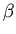 spin. The spatial orbital will be doubly occupied. It is possible
(although sometimes frowned upon) to use one set of spatial orbitals
for spin orbitals with
spin. The spatial orbital will be doubly occupied. It is possible
(although sometimes frowned upon) to use one set of spatial orbitals
for spin orbitals with 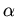 spin and another set for spin orbitals
with
spin and another set for spin orbitals
with 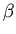 spin.4
spin.4
Where do we get the one-particle spatial orbitals
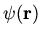 ?
That is beyond the scope of the current section, but we briefly itemize
some of the more common possibilities:
?
That is beyond the scope of the current section, but we briefly itemize
some of the more common possibilities:
- Orbitals centered on each atom (atomic orbitals).
- Orbitals
centered on each atom but also symmetry-adapted to have the correct
point-group symmetry species (symmetry orbitals).
- Molecular orbitals obtained from a Hartree-Fock procedure.
We now explain how an N-electron function
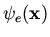 can be
constructed from spin orbitals, following the arguments of Szabo and
Ostlund [4] (p. 60). Assume we have a complete
set of functions of a single variable
can be
constructed from spin orbitals, following the arguments of Szabo and
Ostlund [4] (p. 60). Assume we have a complete
set of functions of a single variable
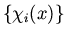 .
Then any
function of a single variable can be expanded exactly as
.
Then any
function of a single variable can be expanded exactly as
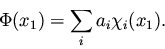 |
(159) |
How can we expand a function of two variables, e.g.
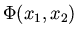 ?
If we hold x2 fixed, then
?
If we hold x2 fixed, then
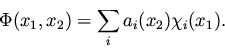 |
(160) |
Now note that each expansion coefficient ai(x2) is a function of a
single variable, which can be expanded as
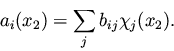 |
(161) |
Substituting this expression into the one for
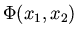 ,
we now have
,
we now have
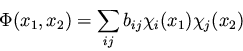 |
(162) |
a process which can obviously be extended for
 .
.
We can extend these arguments to the case of having a complete set of
functions of the variable  (recall
(recall 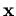 represents x, y,
and z and also
represents x, y,
and z and also 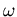 ). In that case, we obtain an analogous result,
). In that case, we obtain an analogous result,
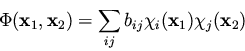 |
(163) |
Now we must make sure that the antisymmetry principle is obeyed.
For the two-particle case, the requirement
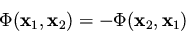 |
(164) |
implies that
bij = -bji and
bii = 0, or
where we have used the symbol
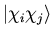 to represent
a Slater determinant, which in the genreral case is written
to represent
a Slater determinant, which in the genreral case is written
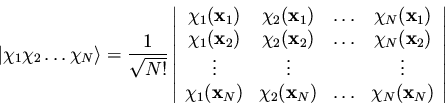 |
(166) |
We can extend the reasoning applied here to the case of N electrons;
any N-electron wavefunction can be expressed exactly as a linear
combination of all possible N-electron Slater determinants formed
from a complete set of spin orbitals
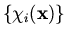 .
.



Next: Matrix Mechanics
Up: Solving the Electronic Eigenvalue
Previous: Solving the Electronic Eigenvalue
![]() .
Why have we been able to avoid including
spin until now? Because the non-relativistic Hamiltonian does not
include spin. Nevertheless, spin must be included so that the
electronic wavefunction can satisfy a very important requirement,
which is the antisymmetry principle (see Postulate 6 in Section
4). This principle states that for a system of fermions, the
wavefunction must be antisymmetric with respect to the interchange of
all (space and spin) coordinates of one fermion with those of
another. That is,
.
Why have we been able to avoid including
spin until now? Because the non-relativistic Hamiltonian does not
include spin. Nevertheless, spin must be included so that the
electronic wavefunction can satisfy a very important requirement,
which is the antisymmetry principle (see Postulate 6 in Section
4). This principle states that for a system of fermions, the
wavefunction must be antisymmetric with respect to the interchange of
all (space and spin) coordinates of one fermion with those of
another. That is,
![]() is to expand it
in terms of a set of one-electron functions, or ``orbitals.'' This
makes the electronic Schrödinger equation considerably easier to
deal with.3 A spin orbital is a function of
the space and spin coordinates of a single electron, while a spatial orbital is a function of a single electron's spatial
coordinates only. We can write a spin orbital as a product of a
spatial orbital one of the two spin functions
is to expand it
in terms of a set of one-electron functions, or ``orbitals.'' This
makes the electronic Schrödinger equation considerably easier to
deal with.3 A spin orbital is a function of
the space and spin coordinates of a single electron, while a spatial orbital is a function of a single electron's spatial
coordinates only. We can write a spin orbital as a product of a
spatial orbital one of the two spin functions
![]() ?
That is beyond the scope of the current section, but we briefly itemize
some of the more common possibilities:
?
That is beyond the scope of the current section, but we briefly itemize
some of the more common possibilities:
![]() can be
constructed from spin orbitals, following the arguments of Szabo and
Ostlund [4] (p. 60). Assume we have a complete
set of functions of a single variable
can be
constructed from spin orbitals, following the arguments of Szabo and
Ostlund [4] (p. 60). Assume we have a complete
set of functions of a single variable
![]() .
Then any
function of a single variable can be expanded exactly as
.
Then any
function of a single variable can be expanded exactly as
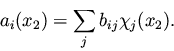
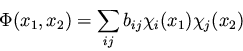
![]() (recall
(recall ![]() represents x, y,
and z and also
represents x, y,
and z and also ![]() ). In that case, we obtain an analogous result,
). In that case, we obtain an analogous result,
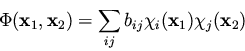
![$\displaystyle \sum_{j > i} b_{ij}
[ \chi_i({\bf x}_1) \chi_j({\bf x}_2) -
\chi_j({\bf x}_1) \chi_i({\bf x}_2) ]$](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img348.png)
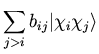
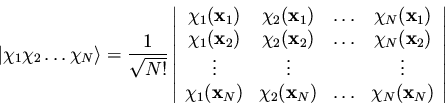
![]() .
.