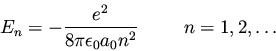


Next: Molecular Quantum Mechanics
Up: Some Analytically Soluble Problems
Previous: The Rigid Rotor
Finally, consider the hydrogen atom as a proton fixed at the origin,
orbited by an electron of reduced mass 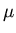 .
The potential due to
electrostatic attraction is
.
The potential due to
electrostatic attraction is
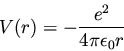 |
(126) |
in SI units. The kinetic energy term in the Hamiltonian is
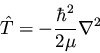 |
(127) |
so we write out the Schrödinger equation in spherical polar coordinates as
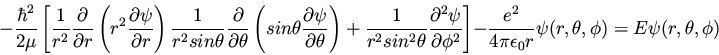 |
(128) |
It happens that we can factor
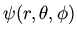 into
into
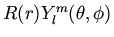 ,
where
,
where
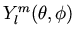 are again the spherical harmonics. The radial part R(r) then can
be shown to obey the equation
are again the spherical harmonics. The radial part R(r) then can
be shown to obey the equation
![\begin{displaymath}- \frac{\hbar^2}{2 \mu r^2} \frac{d}{dr} \left( r^2 \frac{dR}...
...[ \frac{\hbar^2 l(l+1)}{2 \mu r^2} + V(r) - E \right] R(r) = 0
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img263.png) |
(129) |
which is called the radial equation for the hydrogen atom.
Its (messy) solutions are
![\begin{displaymath}R_{nl}(r) = - \left[ \frac{(n - l - 1)!}{2n[(n+l)!]^3} \right...
...^l e^{-r/na_0} L_{n+l}^{2l+1}
\left( \frac{2r}{n a_0} \right)
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img264.png) |
(130) |
where
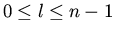 ,
and a0 is the Bohr radius,
,
and a0 is the Bohr radius,
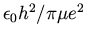 .
The functions
Ln+l2l+1(2r/na0) are the associated
Laguerre functions. The hydrogen atom eigenvalues are
.
The functions
Ln+l2l+1(2r/na0) are the associated
Laguerre functions. The hydrogen atom eigenvalues are
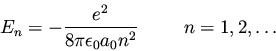 |
(131) |
There are relatively few other interesting problems that can be solved
analytically. For molecular systems, one must resort to approximate
solutions.



Next: Molecular Quantum Mechanics
Up: Some Analytically Soluble Problems
Previous: The Rigid Rotor
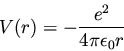
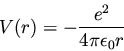
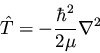
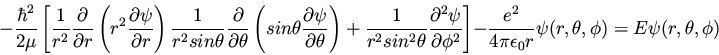
![\begin{displaymath}- \frac{\hbar^2}{2 \mu r^2} \frac{d}{dr} \left( r^2 \frac{dR}...
...[ \frac{\hbar^2 l(l+1)}{2 \mu r^2} + V(r) - E \right] R(r) = 0
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img263.png)
![\begin{displaymath}R_{nl}(r) = - \left[ \frac{(n - l - 1)!}{2n[(n+l)!]^3} \right...
...^l e^{-r/na_0} L_{n+l}^{2l+1}
\left( \frac{2r}{n a_0} \right)
\end{displaymath}](/Quantum%20Mechanics/Tutorial/notes/quantum_doc/img264.png)