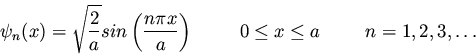


Next: The Harmonic Oscillator
Up: Some Analytically Soluble Problems
Previous: Some Analytically Soluble Problems
Consider a particle constrained to move in a single dimension, under
the influence of a potential V(x) which is zero for
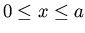 and
infinite elsewhere. Since the wavefunction is not allowed to become
infinite, it must have a value of zero where V(x) is infinite, so
and
infinite elsewhere. Since the wavefunction is not allowed to become
infinite, it must have a value of zero where V(x) is infinite, so
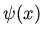 is nonzero only within [0,a]. The Schrödinger equation
is thus
is nonzero only within [0,a]. The Schrödinger equation
is thus
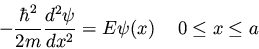 |
(115) |
It is easy to show that
the eigenvectors and eigenvalues of this problem are
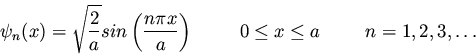 |
(116) |
 |
(117) |
Extending the problem to three dimensions is rather straightforward;
see McQuarrie [1], section 6.1.